Secret Sharing

Secret Splitting

Given a secret s, we would like n parties to share the secret so that the following properties hold:

1. All n parties can get together and recover s.

2. Less than n parties cannot recover s.

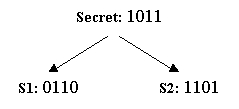
We can easily generalize the scheme for cases where there are n parties: we generate n-1 random bit strings (with the same number of bits as the secret) as the first n-1 shares. The last share is the result of bitwise XORing the secret with all the other n-1 shares.

(n,t) Secret Sharing

Given a secret s, to be shared among n parties, that sharing should satisfy the following properties:

1. Availability: greater than or equal to t parties can recover s.

2. Confidentiality: less than t parties have no information about s.

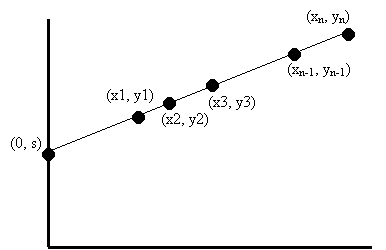
To generalize the scheme even further, we have a construction of an (n, t) secret sharing scheme. Now we use the curve that corresponds to a (t-1) degree polynomial:

$$y=a_{t-1} * x^{t-1} + a_{t-2} * x^{t-2} + ... + a_1 * x + a_0$$

We randomly select a curve corresponding to such a polynomial that goes through the secret on the y-axis. And then we select n points on the curve. Using the same arguments, we can show that this scheme satisfies both availability and confidentiality properties. (Note: this scheme was invented by Shamir in 1979. The original scheme was defined on a finite field.)

Online Secret Sharing

How to rely on the servers themselves to do re-sharing in a distributed manner after being compromised. No server can ever reconstruct the secret because otherwise the secret could be exposed if the server was compromised.

Proactive Secret Sharing (PSS)

A scheme that allows servers to generate a new set of shares for the same secret from the old shares without reconstructing the secret. In reality, break-ins to a server are very hard to detect. To strengthen the security of a replicated service, we can invoke our PSS periodically (at regular intervals).

The proactive secret sharing between two servers can be performed in the following steps:

1. Server 1 generates two subshares $s_{11}$ and $s_{12}$ from its share $s_1$ using the same secret sharing scheme as the one used to generate $s_1$ and $s_2$ from s; that is, server 1 randomly selects two subshares $s_{11}$ and $s_{12}$, so that $s_1 = s_{11} + s_{12}$. Server 2 does the same thing to $s_2$: It randomly generates two subshares $s_{21}$ and $s_{22}$, so that $s_2 = s_{21} + s_{22}$.

2. Server 1 sends $s_{12}$ to server 2 through a certain secure channel. Server 2 sends $s_{21}$ to Server 1.

3. Server 1 has both $s_{11}$ and $s_{21}$ and can add them up to get a new share $s_1' = s_{11} + s_{21}$. Server 2, on the other hand, has both $s_{12}$ and $s_{22}$ and can generate a new share $s_2' = s_{12} + s_{22}$. Now we show that $s_1'$ and $s_2'$ constitute a (2, 2) sharing. The sum of these two shares is the sum of all the four subshares, which is the sum of $s_1$ and $s_2$, which is s.

These two shares are independent from the old ones because these subshares are generated randomly. Also, no server knows the secret during the entire process. Server 1 generates $s_{11}$ and $s_{12}$ and learns $s_{21}$ from server 2, but server 1 never knows $s_{22}$ and thus does not know $s_2'$ or s. Server 2, on the other hand, never knows $s_{11},$ and thus does not know $s_1'$ or s.

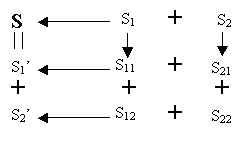
Proactive (n, t) Secret Sharing

Single Server h(x)

For an (n, t) sharing, the original secret function is: $f(x)=a_{t-1} * x^{t-1} + a_{t-2} * x^{t-2} + ... + a_1 * x + s$

1. A server selects a function $h(x)=b_{t-1} * x^{t-1} + b_{t-2} * x^{t-2} + ... + b_1 * x$.

2. For each $1\le i \le n$, the server computers $h(i)$ and sends $h(i)$ to server $i$ (through secure channel).

3. The new curve where the new shares are selected corresponds to function $f'(x)=f(x)+h(x)$. Server i then computes the new share $s_i'=f'(i)=f(i)+h(i)$.

Decentralized Manner

However, this extension has a severe security flaw. In cases where $t > 2$, it is not enough to let only one server select $h(x)$: if the server that picks $h(x)$ is compromised during PSS, then the adversary may know the relationship between new shares and old shares.

As a countermeasure, we ask $(t-1)$ servers to select $(t-1)$ different $h(x)$ functions:

1. Server $j\space (1 \le j \le t-1)$ selects randomly a function $h_j(x)=b_{(j,t-1)} * x^{t-1} + b_{(j,t-2)} * x^{t-2} + ... + b_{(j,1)} * x$.

2. Sever $j$ then computes $h_j(i)$ and sends $h_j(i)$ to server $i$ (for each $1 \le i \le n$).

3. The new curve where the new shares are going to be selected corresponds to the function $f'(x)=f(x)+\sum_{j=1}^{t-1} h_j(x)$. Therefore, each server i computes the new share $s_i'=f'(i)=f(i)+\sum_{j=1}^{t-1} h_j(i)$.

References:

https://www.cs.cornell.edu/courses/cs513/2000SP/SecretSharing.html